
This is given by r2 which is the square of the Correlation > Pearsons Coefficient This measures the proportion of the variation in the independent variable. One statistic that can be used as an indication is the coefficient of determination. The values of a and b that minise the squared errors is given by the following equation:īefore a regression equation can be used effectively you need to see how well it fits the data. You must always make sure that the y-variable is the dependent variable in the equation: Linear regrssion involves finding the line that minimises the sum of the squares of the errors. Squaring the errors not only removes the sign but also gives more emphasis to the larger errors. The absolute values of the errors could be added up but the line of best fit is obtained when the sum of the squares of the errors is as small as possible. This doesn't prove that the line is a good one though. If you add these errors together you will find that they total zero. The errors above the line are positive and the errors below the line are negative. These differences are often referred to as errors. You could find the difference between each point and the line. Produces the slope of a line that best fits a single set of data. This is the simplest form of equation between two variables.

The technique of linear regression attempts to define the relationship between the dependent and independent variables by means of a linear equation. LINEST - used to project an exponential curve RSQ - The square of the Pearson product moment correlation coefficient (ie coefficient of determination) This is a type of bivariate descriptive function. SLOPE - The slope of the linear regression.
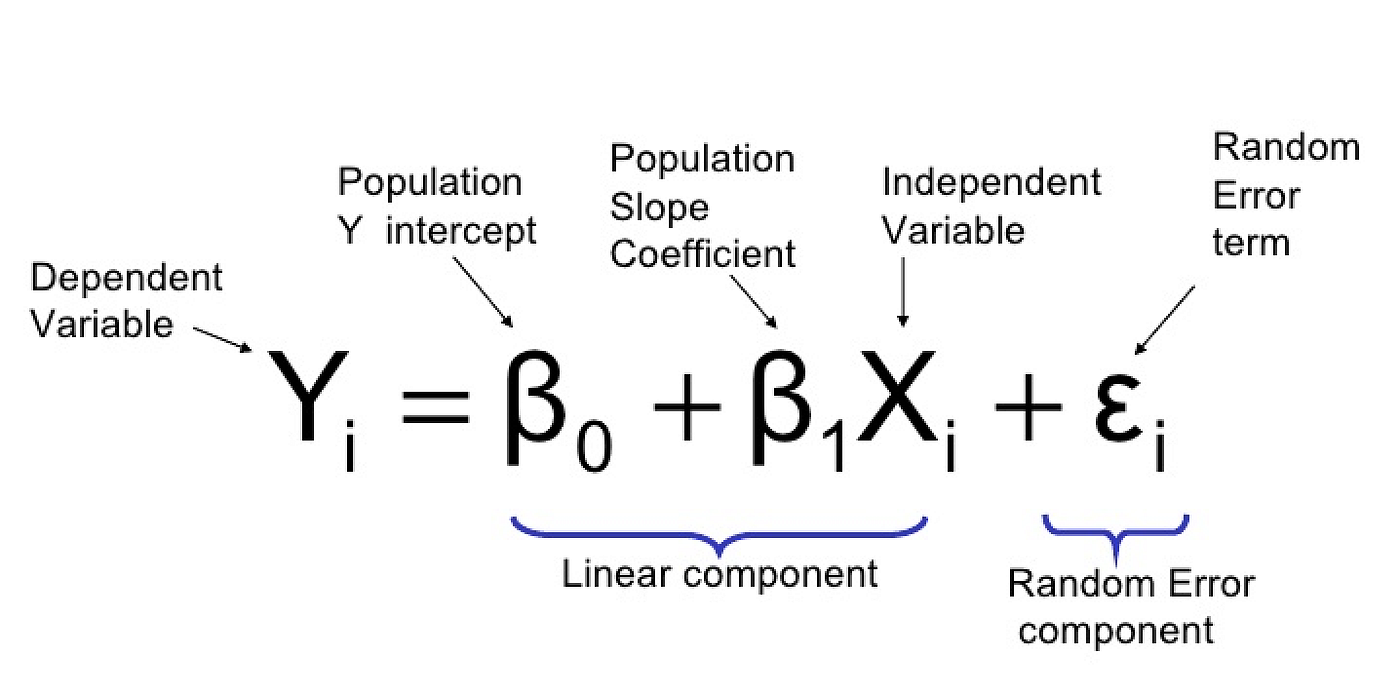
The regression function can lie in a specified set of functions which may be infinite in dimension

The regression function is defined in terms of a finite number of unknown parameters that are estimated from the data In some circumstances, regression analysis can be used to infer "casual" relationships between the dependent and independent variables Regression analysis is widely used for prediction and forecasting It is also common to characterise the variation of the dependent variable around the regression function which can be described by a probability distribution The estimation target is a function of the independent variables called the "regression function" Regression analysis estimates the conditional expectation (ie average value) of the dependent variable, given the independent variables These techniques help you understand how the dependent variable changes when one of the independent variables change (while the other independent variables remain the same) There are various techniques for analysing the relationship between dependent and independent variables


 0 kommentar(er)
0 kommentar(er)
